Quantum Algorithms and Simulation
We are interested in efficient, scalable, and robust simulation of complex physical and chemical processes on quantum computers, focusing on long-term fault-tolerant algorithms. This line of research will elucidate the intricate interplay between correlated electronic, vibrational, and dissipative processes that underpins fundamental aspects of chemistry and physics. Targeting applications include microscopic mechanisms of photosynthetic processes, quantum material design, and chemical reaction pathways in complex systems. We are also interested in analyzing robustness and parallelism in quantum algorithms.
Quantum Simulation of Physical Sciences
Theoretical physical sciences (chemistry, condensed matter physics, and biology) have made tremendous progress towards modeling physical processes, largely by relying on classical algorithms and computational resources. However, Nature is inherently quantum, and it is critical to harness quantum resources to simulate and understand physical processes. Quantum computers provide enormous computational power, while the best ways to use them for simulating physical sciences remain unclear. We develop novel paradigms to tackle both
Electronic Structure
Real-Time Dynamics
Finite-Temperature and Extended Systems
Electronic structure theory studies the eigenstates and eigenenergies of many-electron interacting systems. Exact solutions of electronic structure on classical computers are intractable for large systems. We are interested in potential quantum advantages of quantum computers for such problems.
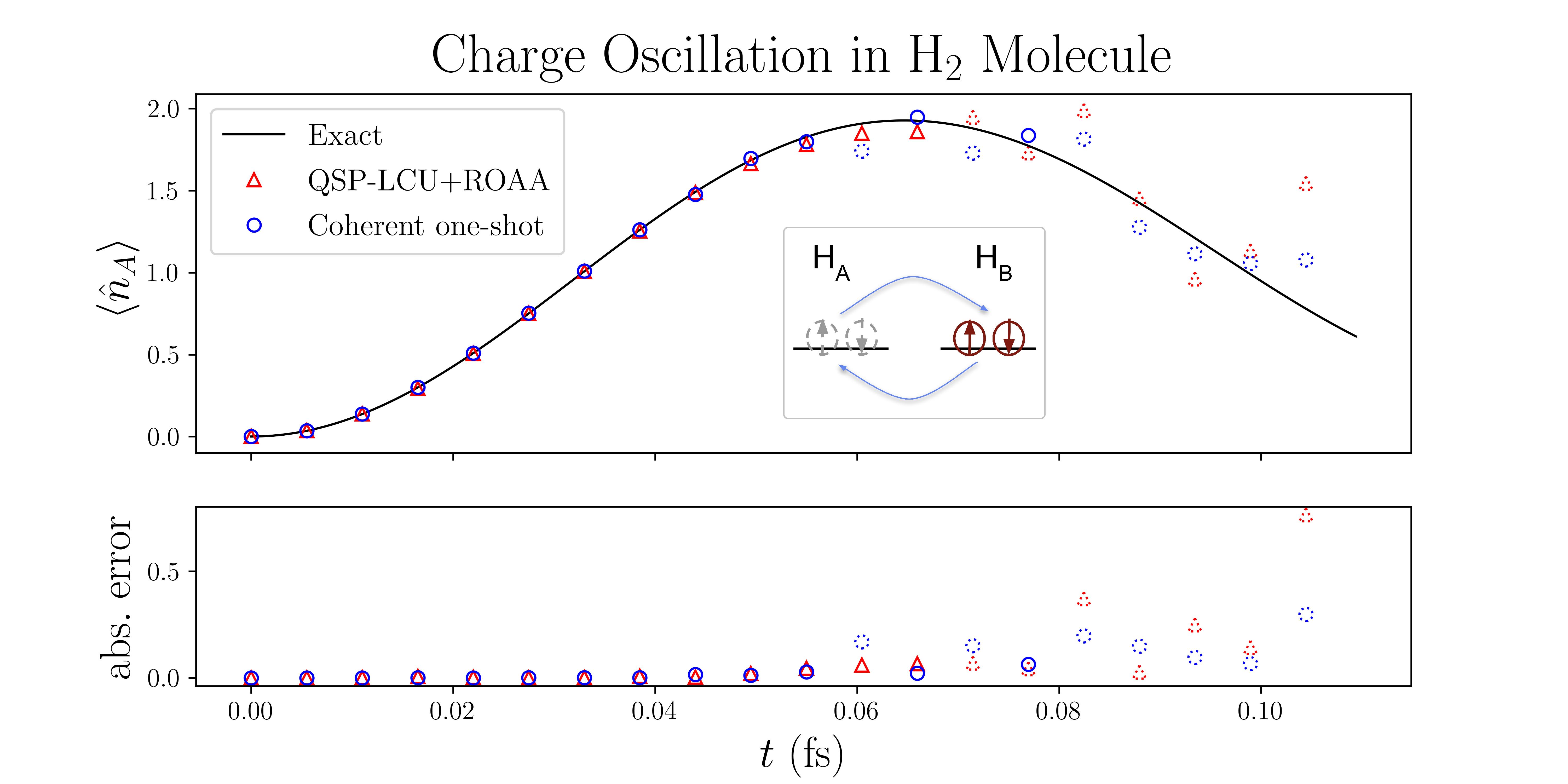
Real-time dynamics (Hamiltonian simulation) of interacting quantum systems are notoriously difficult on classical computers but they can be efficiently simulated on quantum computers. We are interested in developing efficient Hamiltonian simulation algorithms based on hybrid qubit-bosonic quantum resources to solve practical chemistry problems that are relevant to photosynthesis and catalysis, which often involve both electron and nuclei motion.
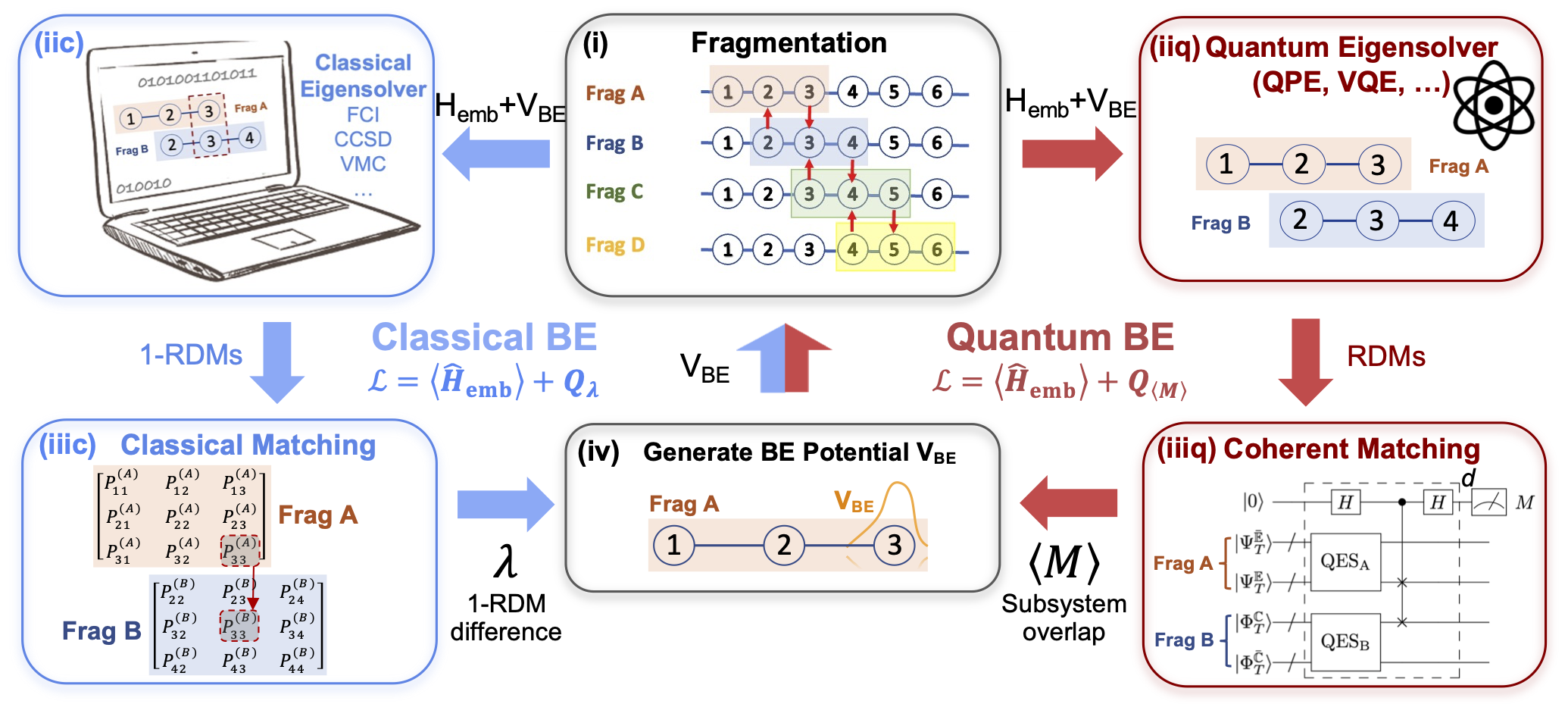
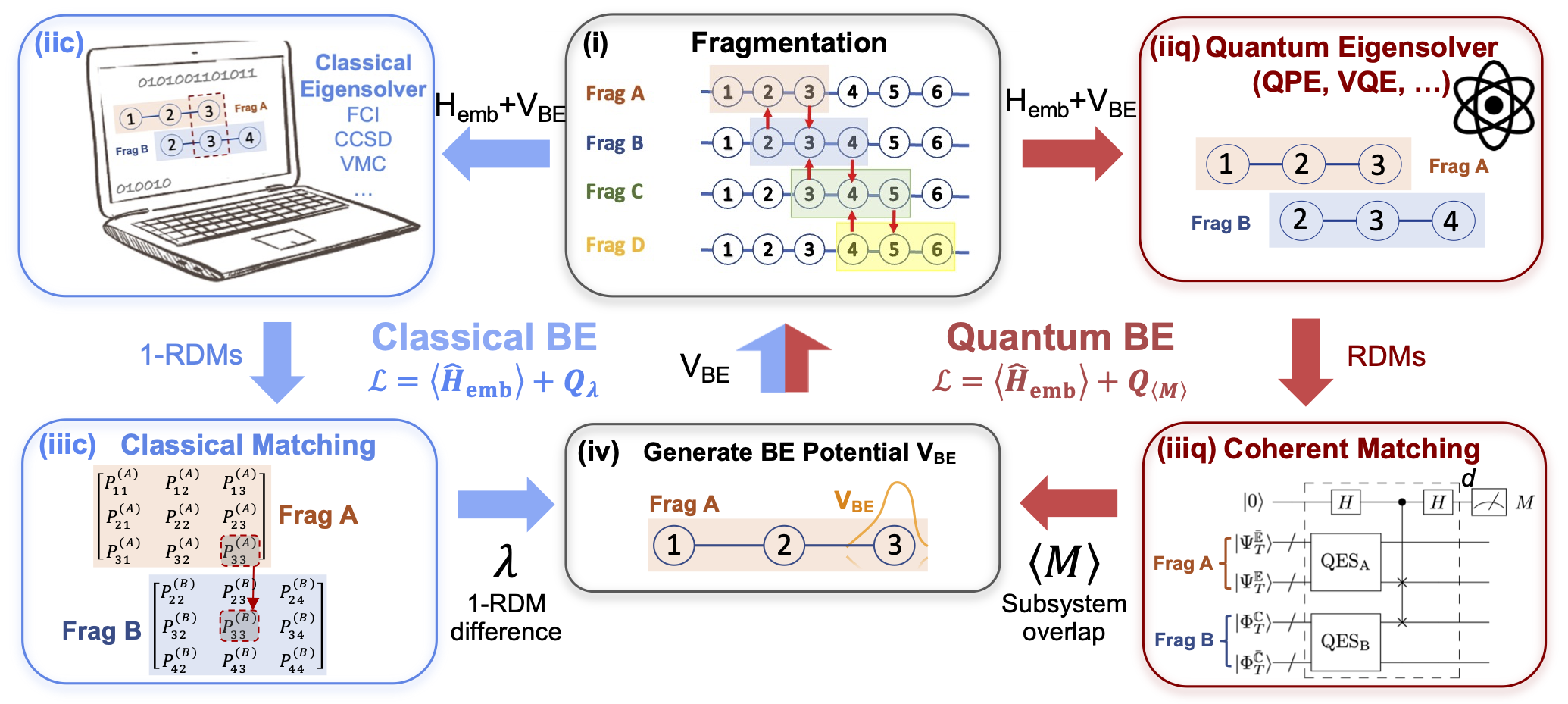
We are also interested in simulating statistical properties of interacting quantum systems at a finite temperature. We aim to integrate state-of-the-art classical algorithms (such as quantum Monte Carlo) and quantum subroutines to enable efficient simulation of extended systems such as quantum materials with unprecedented accuracy and efficiency.

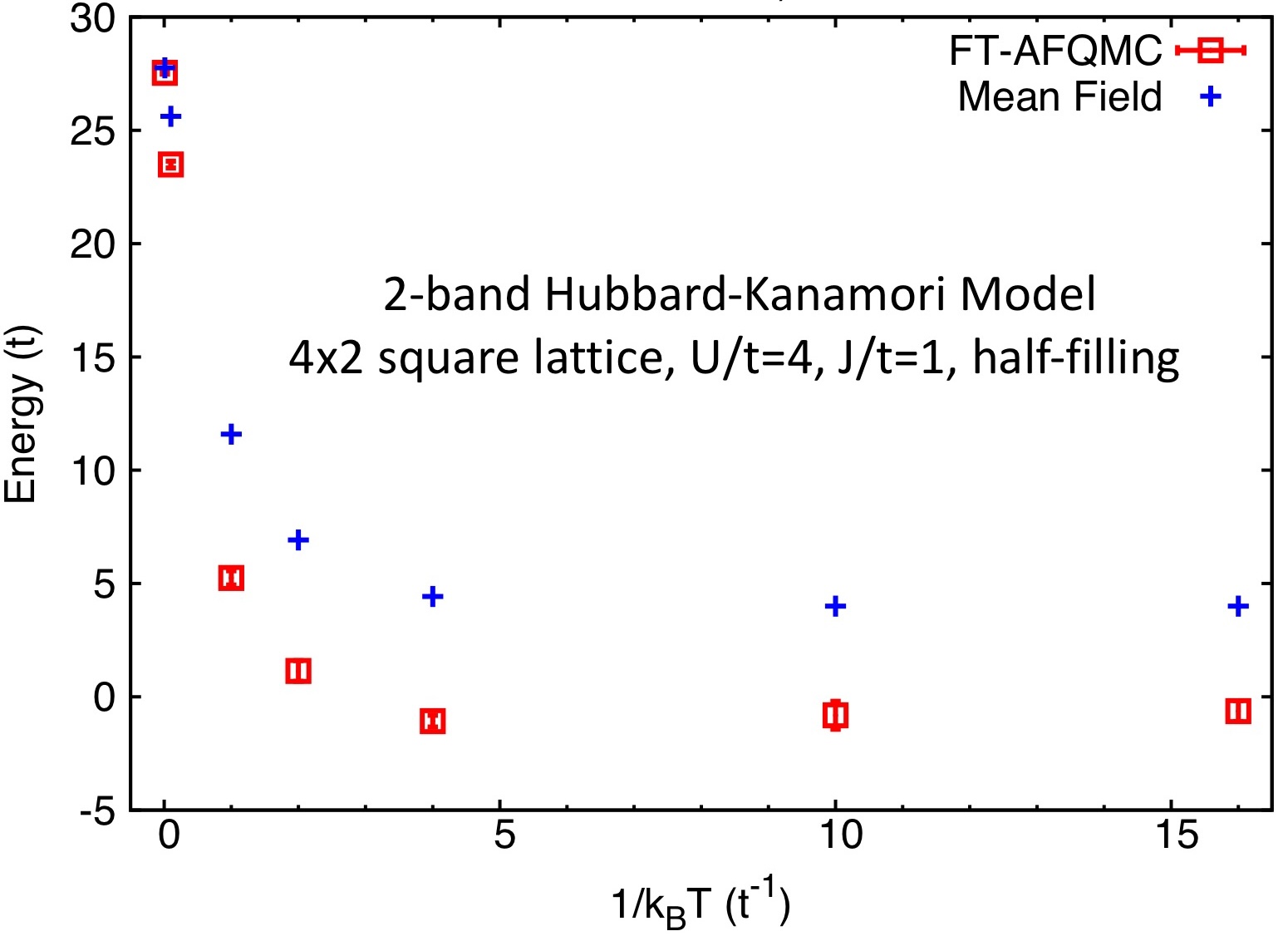
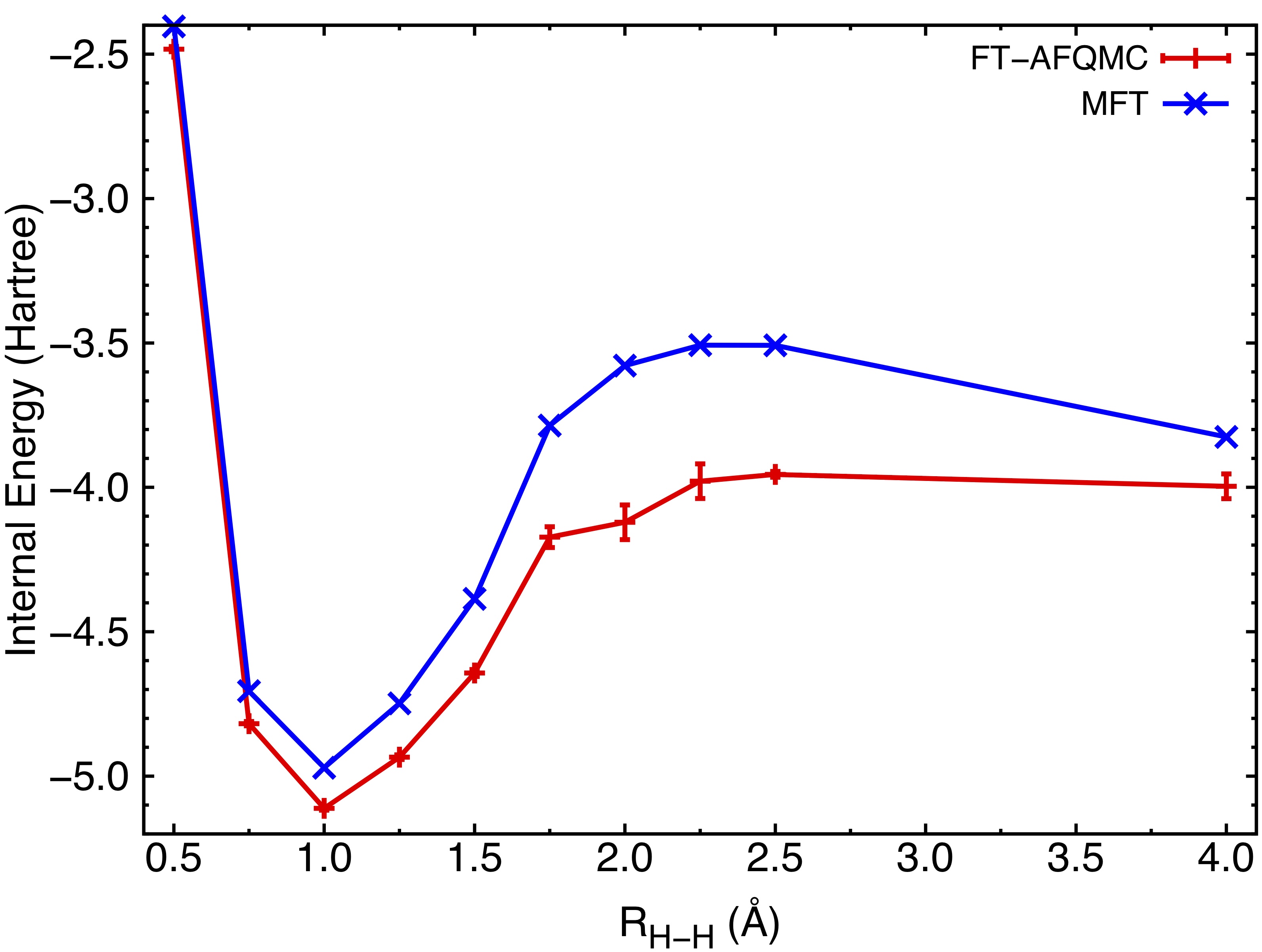
Robustness of Quantum Algorithms
The intrinsic probabilistic nature of quantum systems makes error correction or mitigation indispensable for quantum computation. While current error-correcting strategies focus on correcting errors in quantum states or quantum gates, these fine-grained error-correction methods can incur significant overhead for quantum algorithms of increasing complexity. We are interested in exploring novel ways to build robustness into quantum algorithms at a coarse-grained or system level.
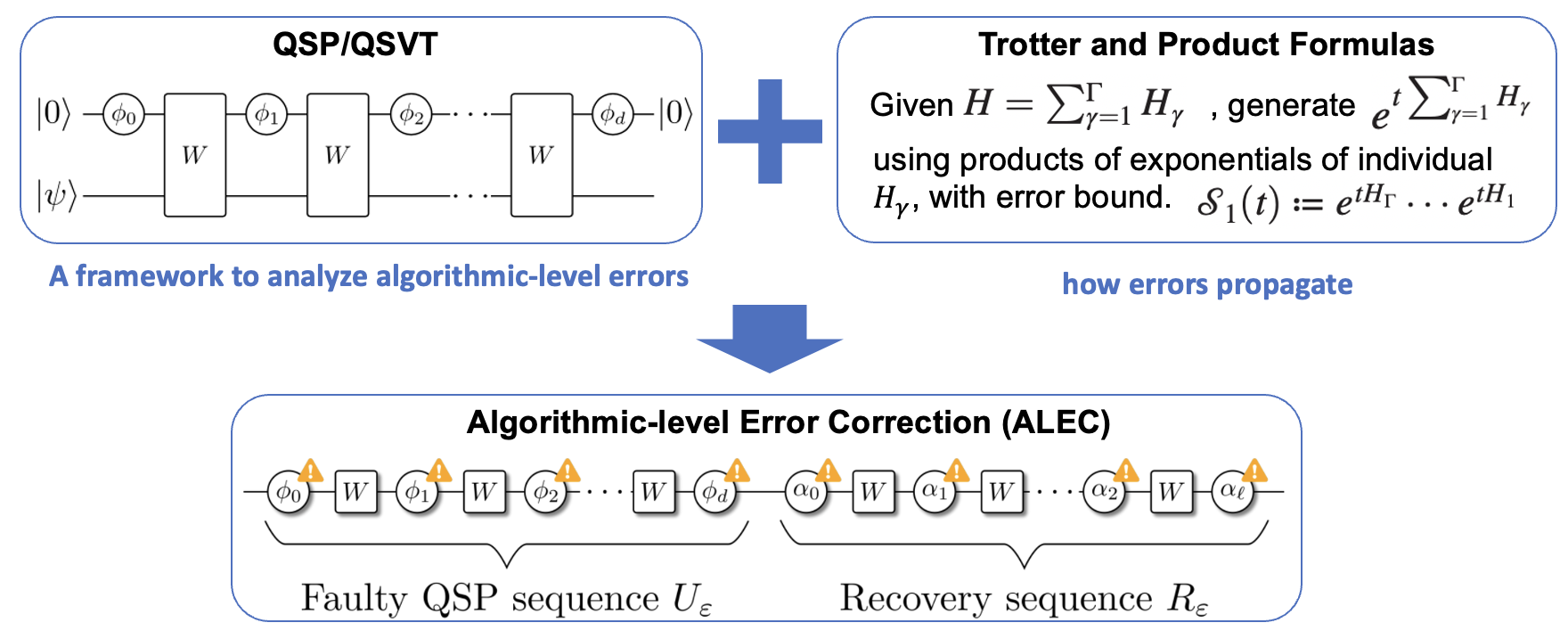
References
2024
-
 Quanta-Bind: A quantum computing pipeline for strongly correlated systems for Alzheimer’s diseaseIn 2024 IEEE International Conference on Quantum Computing and Engineering (QCE), 2024
Quanta-Bind: A quantum computing pipeline for strongly correlated systems for Alzheimer’s diseaseIn 2024 IEEE International Conference on Quantum Computing and Engineering (QCE), 2024