Hybrid Continuous-Discrete Variable Quantum Computing

Conventionally, quantum information science studies the control of discrete-variable (DV) systems such as qubits. Continuous-variable (CV) systems such as bosonic modes are ubiquitous in Nature (such as molecular vibrations, phonons in solid materials, photons in optics) and yet much less is known on how to control and utilize them. We develop full-stack theories, algorithms, protocols, and architectures to simultaneously manipulate multiple bosonic modes and qubits to fully unleash the potential of hybrid CV-DV quantum computing for various applications.

 

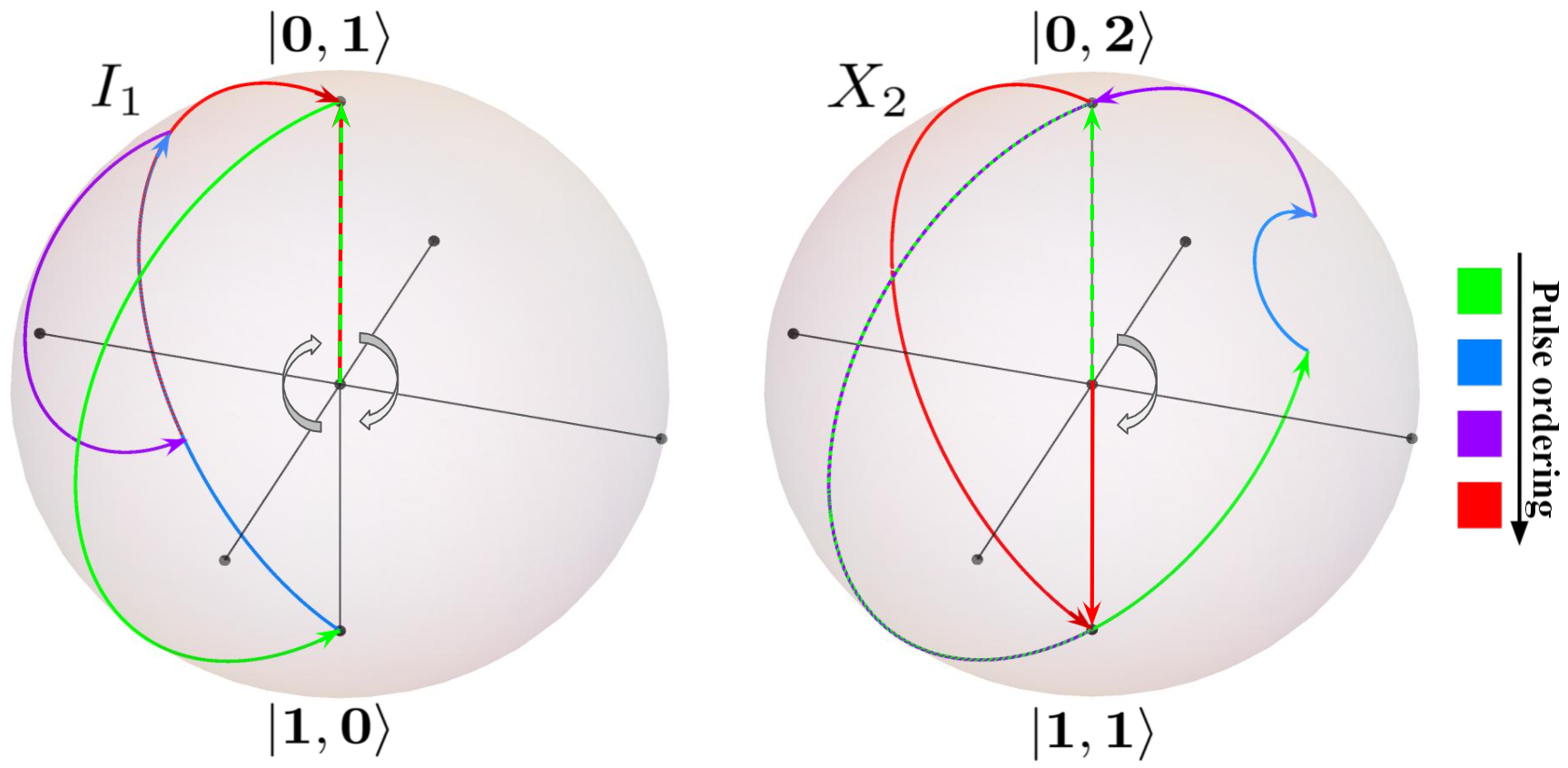
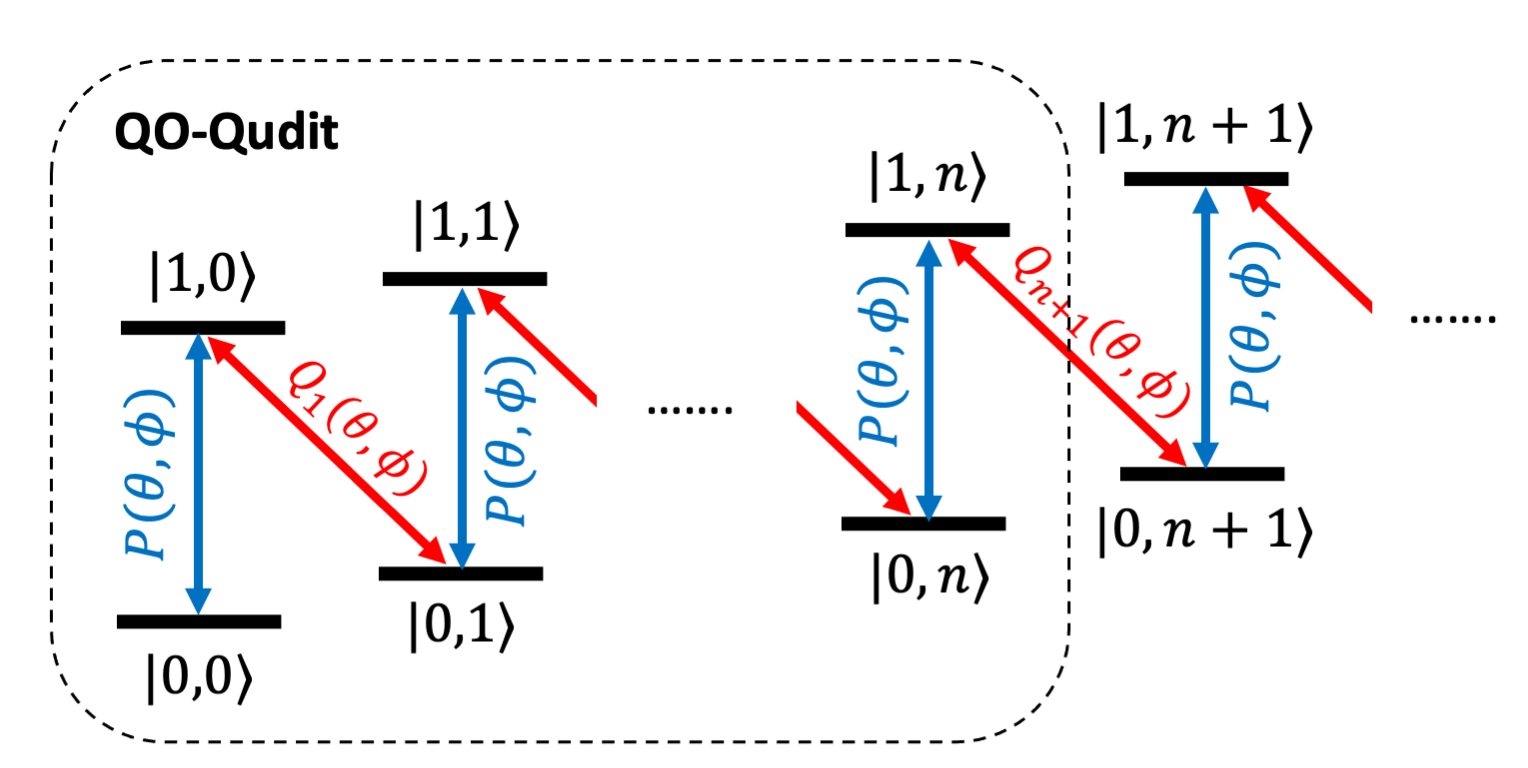
Qubit-Oscillator Qudit

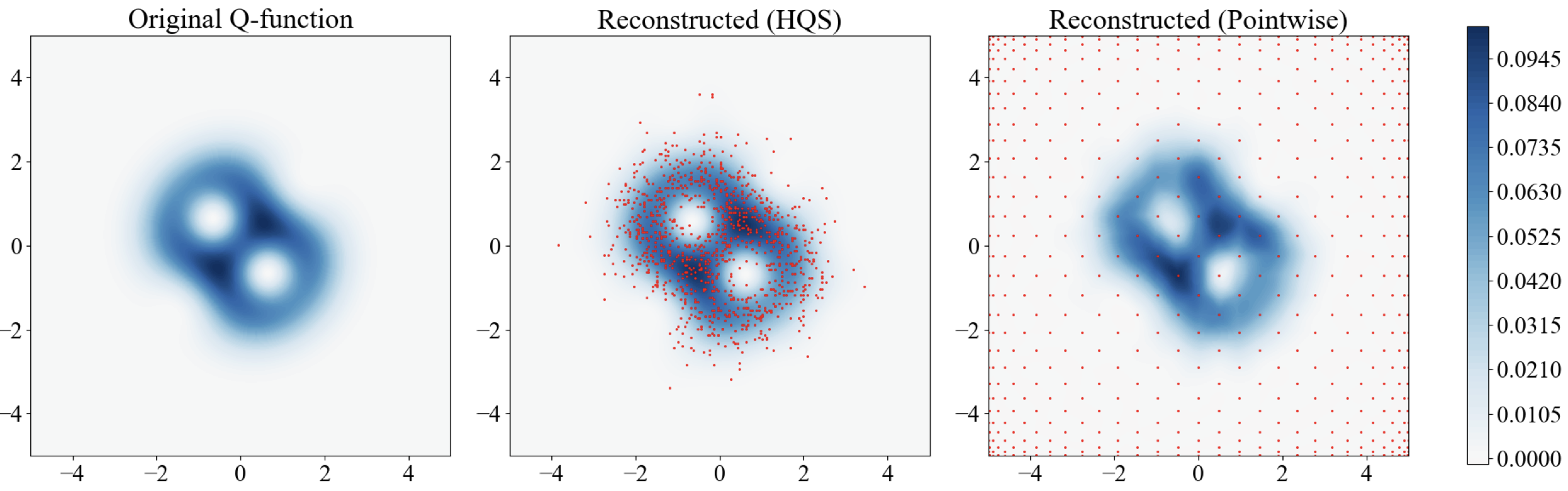
Bosonic modes (quantum harmonic oscillators) provide vast hardware-efficient quantum resources because even a single bosonic mode can be used as a multi-level quantum system. We are interested to design quantum control protocols to harnessing these continuous-variable bosonic systems for quantum computation, by constructing finite dimensional qudits from an oscillator using simple Jaynes-Cummings interactions, which is readily implementable on trapped ion quantum computers.

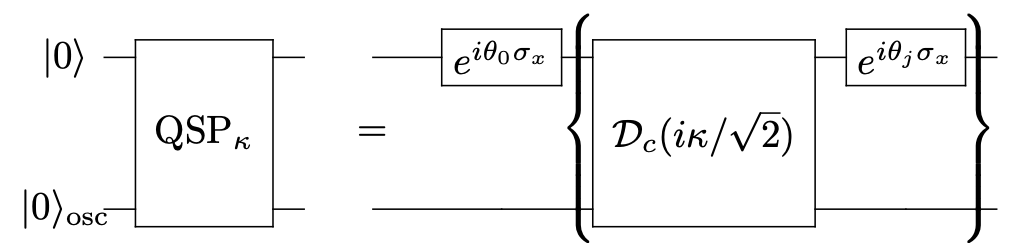
Energy level diagram in a \(d\)-QO-qudit. The first index in the state label represents the qubit state and the second represents the oscillator Fock level. Arrows indicate control pulses that couples different states.
A 24-pulse realization of the \(-I \oplus -I \oplus -X\) operation in the lowest 3 subspaces (from left to right, \(\{\ket{0,1} \leftrightarrow \ket{1, 0} \}, \{\ket{0,2} \leftrightarrow \ket{1,1}\}, \{\ket{0,3} \leftrightarrow \ket{1,2}\} \))

 

Hybrid CV-DV Quantum Algorithms

Designing better quantum algorithms has been one of the central pursuits of quantum computation. Hybrid CV-DV quantum systems provide novel playground for quantum algorithm design. We are interested in generalizing major quantum algorithmic primitives such as quantum signal processing (QSP), linear combination of unitaries (LCU), and product formulas from DV to hybrid CV-DV quantum computers. These new hybrid CV-DV quantum algorithms bring significant insights and quantum advantages to quantum computation, quantum simulation (boson-fermi mixed matter), quantum control, quantum error-correction, among many other applications.

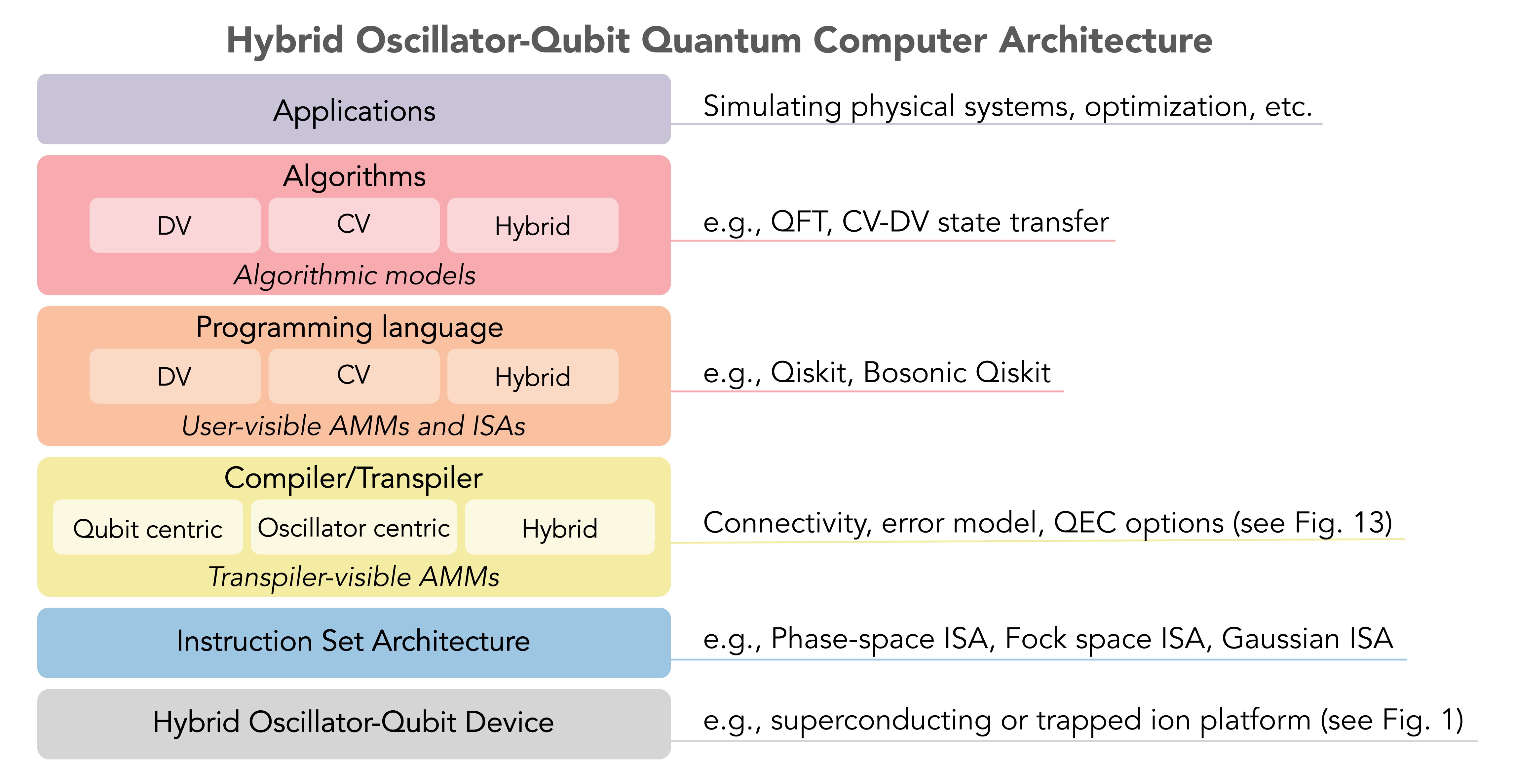
A single-variable hybrid CV-DV QSP circuit composed of single-qubit rotations and controlled displacement operations. The gates inside the bracket are repeated \(d\) times for different \(\theta_j~ (j = 1, 2, \cdots, d)\) in order to obtain a degree-\(d\) Laurent polynomial.

 

Hybrid CV-DV Quantum Processors and Architectures

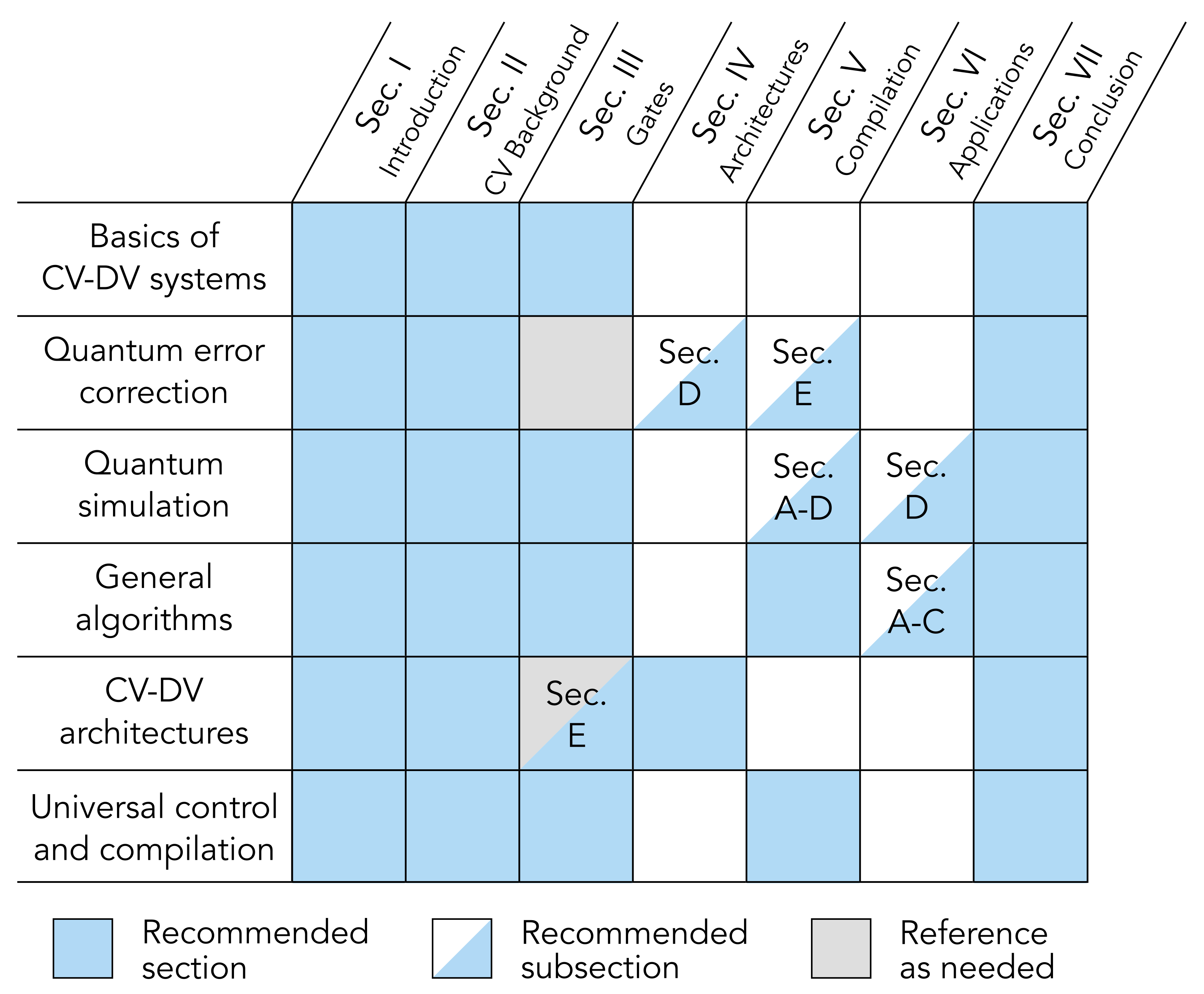
Just like quantum algorithms, hybrid CV-DV quantum processors opens a variety of possibilities for architecture and compiler design across the full quantum computing stack. We are interested in exploring new abstract machine models (AMMs) and instruction set architectures (ISAs) for these novel quantum computers.

Schematic illustration of hybrid CV-DV hardware and its abstraction. See our bosonic ISA paper for more details.

References

2024

  1. readersguide.png
    Hybrid Oscillator-Qubit Quantum Processors: Instruction Set Architectures, Abstract Machine Models, and Applications
    Yuan Liu*, Shraddha Singh*, Kevin C Smith*, Eleanor Crane, John M Martyn, Alec Eickbusch, Alexander Schuckert, Richard D Li, Jasmine Sinanan-Singh, Micheline B Soley, and  others
    2024
    arXiv PDF

2021

  1. QOQ.png
    Constructing qudits from infinite-dimensional oscillators by coupling to qubits
    Yuan Liu\(^\dagger\), Jasmine Sinanan-Singh, Matthew T Kearney, Gabriel Mintzer, and Isaac L Chuang
    Physical Review A, 2021
    HTML PDF