Hybrid Discrete-Continuous Variable Quantum Information Processing
Conventionally, quantum information science studies the control of discrete-variable (DV) systems such as qubits. Continuous-variable (CV) systems such as bosonic modes are ubiquitous in Nature (such as molecular vibrations, phonons in solid materials, photons in optics) and yet much less is known on how to control and utilize them. We develop rigorious theories and efficient schemes to simultaneously manipulate multiple bosonic modes and qubits in a hybrid fashion to fully unleash the potential of hybrid DV-CV computation and quantum information processing.
Qubit-Oscillator Qudit
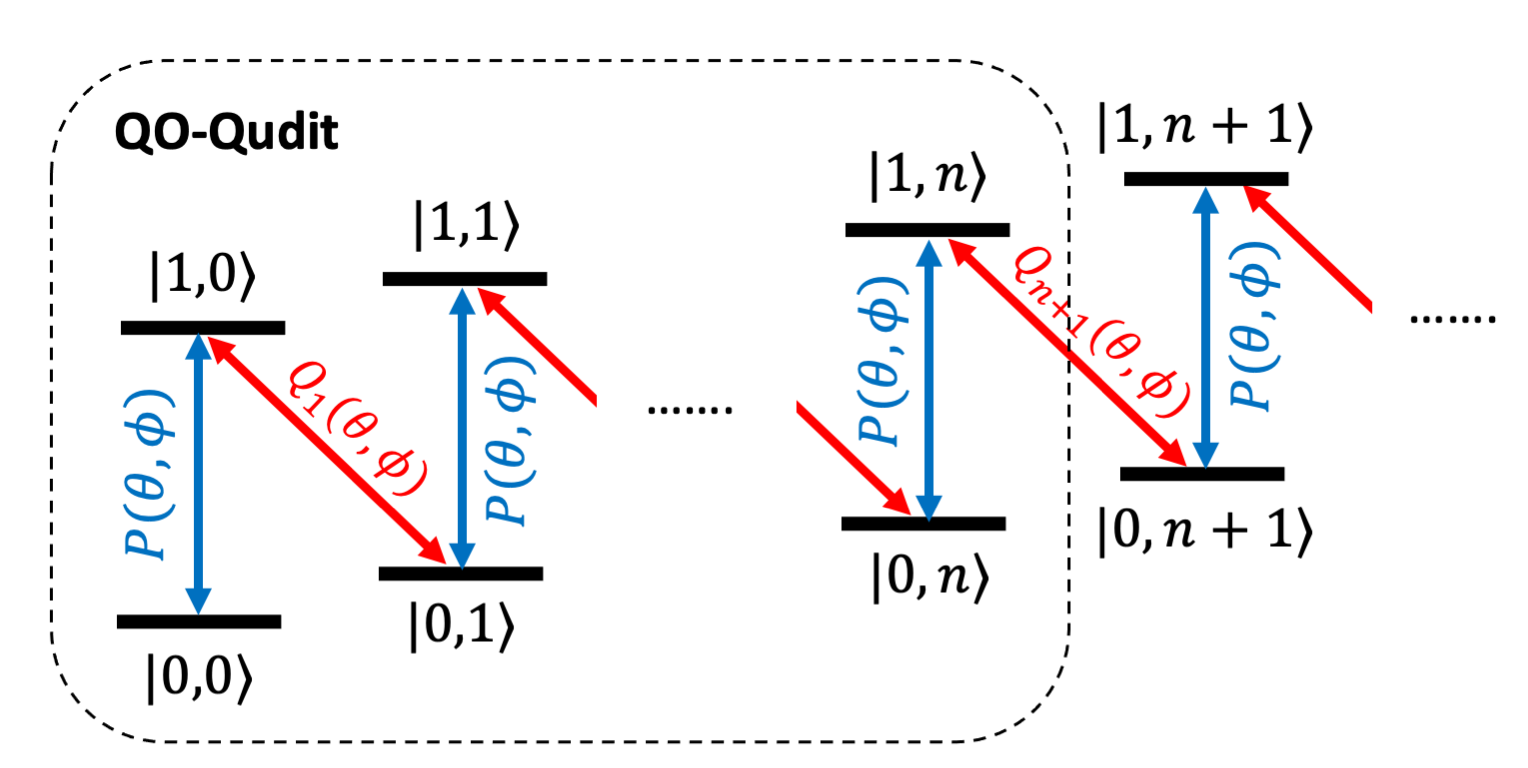
Bosonic modes (quantum harmonic oscillators) provide vast hardware-efficient quantum resources because even a single bosonic mode can be used as a multi-level quantum system. We are interested to design quantum control protocols to harnessing these continuous-variable bosonic systems for quantum computation, by constructing finite dimensional qudits from an oscillator using simple Jaynes-Cummings interactions, which is readily implementable on trapped ion quantum computers.
Hybrid CV-DV Quantum Signal Processing
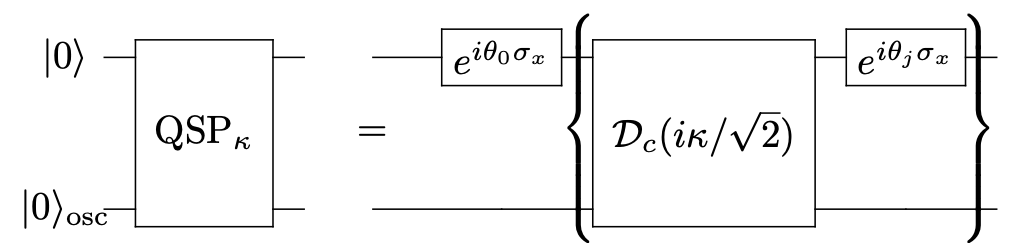
Quantum signal processing (QSP) relies on two components: i) a block-encoding of the operator; and ii) the ability to impart an arbitrary phase shift to the encoded operator. Block-encoding in simply means embedding the target operator inside a unitary matrix. Methods for block-encoding on qubit devices are mostly limited and block-encoding of a general Hamiltonian is difficult. It might thus seem that such block-encoding will be especially challenging for infinite dimensional bosonic oscillators. Surprisingly, some physical interactions between qubits and oscillators can provide natural block-encodings. This allows qubitization of bosonic modes and generalization of QSP to hybrid CV-DV systems. We are interested to develop such hybrid CV-DV QSP into powerful framework to control and compile useful operations on hybrid qubit-oscillator quantum processors.